|
Your task is to solve the eight-queens puzzle in
Funnel. The eight-queens puzzle asks how to place eight
queens on a chessboard so that no queen is in check from
any other; i.e. no two queens are in the same row, column,
or diagonal.
One possible solution is illustrated in the following
figure:
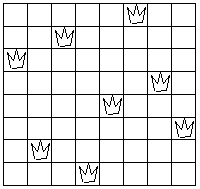
One way to solve the puzzle is to work across the board,
placing a queen in each column. Once we have placed k - 1
queens, we must place the kth queen in a position
where it does not check any of the queens already on
the board. This approach can be formulated as a recursive
algorithm: Assume that we have already generated the sequence
of all possible ways to place k - 1 queens in the
first k - 1 columns of the board. For each of these
ways, generate an extended set of positions by placing
a queen in each row of the kth column. Now filter
these, keeping only the positions for which the queen
in the kth column is safe with respect to the other
queens. This produces the sequence of all qays to place
k queens in the first k columns. By continuing
this process, we will produce not only one solution, but
all solutions to the puzzle.
This solution can be implemented with a function queens,
which returns a sequence of all solutions to the problem of
placing n queens on an n x n chessboard.
def queens(n) = {
val rows = List.enum(1, n)
def queenCols(k) = {
if (k == 0)
List.make(empty)
else
queenCols(k - 1)
.map(pos| rows.map(row| adjoin(row, k, pos))
.concat
.filter(pos| safe(k, pos))
}
queenCols(n)
}
Complete this program by implementing the representation
for sets of board positions, including the function
adjoin, which adjoins a new row/column position
to a set of positions, and empty, which represents
an empty set of positions. You must also write the function
safe, which determines for a set of positions,
whether the queen in the kth column is safe with
respect to the others.
[Source: Abelson, Sussman "Structure
and Interpretation of Computer Programs"]
